skip to content W3C SVG

Dark Crystal Key Backup Protocol Specification

1 Introduction

Dark Crystal is a social key management system. It is a set of protocols and recommendations for responsibly handling sensitive data such as secret keys.

It is designed for safeguarding data which we don’t want to loose, but which we don’t want others to find.

The idea is that rather than creating a generalised piece of software for managing keys, key management techniques should be integrated into the applications which use the keys. So the techniques described and libraries provided can be seen as recommendations for developers wanting to improve key management for particular applications. Of course, every situation is different and in many cases the protocol will need to be adapted for particular needs.

This document describes a social key backup and recovery technique, to enable lost keys, passwords or other sensitive data to be recovered, using a small group of trusted contacts.

It must be emphasised that key recovery cannot solve the problem of compromised keys. It is appropriate only to recover encrypted data following loss of a key, or for continued use of a key when it is known to be lost but not compromised, for example following accidental deletion or hardware failure.

2 Terms used

  • Secret - the data to be backed up and potentially recovered.
  • Secret-owner - the peer to whom the data belongs and who initiates the backup.
  • Shard - a single encrypted share of the secret.
  • Custodian - a peer who holds a shard, generally a friend or trusted contact of the secret owner.

3 Key Loss Scenarios

These scenarios will be discussed in greater depth in the report on social factors. But it is important to already make the distinction between the three main kinds of key loss:

  • ‘Swim’ - key loss - For example, the computer fell into the sea and is lost forever. In the case the key is assumed lost, but not compromised.
  • ‘Theft’ - key compromise - For example, I forgot my computer on a train and have no idea who might have it. The key is both lost and compromised.
  • ‘Inheritance’ - following death, incapacitation or imprisonment, a key can be recovered by heirs. This covers any situation where custodians recover the secret without the involvement of the secret owner.

4 Who is this for?

This protocol is designed to be integrated into applications which deal with sensitive data or where effective key management is critical.

The protocol is agnostic to transport and storage mechanisms, meaning messages used for this backup system can be transmitted and stored in the same way your application handles other types of data. The benefit of this is that it should be easy to integrate, and not require too many additional dependencies.

However, when deciding whether this protocol is a good fit for your application, several factors need to be taken into account. These are discussed in more detailed in our ‘Threat modelling’ and ‘Social factors’ reports.

The architecture of the application has an effect on how effective these techniques are. This backup technique is robust because of its distributed nature. Ideally, shards are stored in multiple locations controlled by multiple ‘custodians’. If the application uses a traditional client-server architecture, there is a concern that all shards are stored on the same server, meaning the same physical location.

This is perhaps be not as bad as it sounds, since each shard would be encrypted to a particular custodian, and the custodian’s secret key should be stored only on their client device. But it is far from ideal, as a compromised server would mean a metadata leak as well as a possibility that the shards could be lost.

So while it is possible, though not advised, to use a centralised server to coordinate communication between peers, it must be emphasised that shards must be stored locally on client devices. Reliance on a particular server is analogous to “putting all your eggs in one basket”, and detracts from the core principle of this protocol, which is to provide a distributed backup.

5 Peer experience

This is a technical specification of the protocol. Many stages of the process will be automated and not visible to the peers. Interface recommendations and peer stories will be described elsewhere.

6 Cryptographic primitives

6.1 Introduction

Standards are generally adopted from the Networking and Cryptography library (NaCl). These were chosen because they are widely adopted and regarded to be secure, and available in a wide variety of high level languages, either through bindings to the C library ‘libsodium’ (which is based on NaCl), or by high level implementations which are based on the same cryptographic parameters and algorithms and can reproduce the same behaviour in tests.

6.2 Notation used

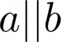
concatenation

Concatenation of a and b

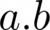
scalar multiplication

Deriving a shared key from keys a and b by scalar multiplication

box

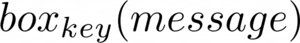
Authenticated encryption of message with key

HMAC

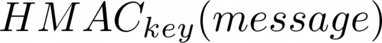
Keyed hash of message

6.3 Authenticated Symmetric Encryption

The symmetric encryption algorithm used is NaCl’s ‘secretbox’, which consists of the XSalsa20 stream cipher, and a poly1305 message authentication code, both developed by Daniel J. Birnstein. These were chosen because they are widely adopted and regarded to be secure.

We encode encrypted messages as the nonce concatenated with the MAC, concatenated with the ciphertext:

nonce MAC ciphertext

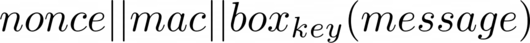
Since the nonce used by XSalsa20 is 24 bytes and the MAC used by Poly1305 is 16 bytes, ciphertext messages are plaintext length + 24 + 16 bytes long.

External documentation links:

6.4 Signing and Verification

Signing is achieved using the Edwards curve digital signature algorithm (EdDSA), using recommended parameters for the Ed25519 and Ed448 elliptic curves.

External documentation links

6.5 Public Key Encryption

An agreement (shared secret) is calculated using Curve25519 keypairs. Both public and private keys are 32 bytes long.

Because of the way scalar multiplication works, the space of possible DH agreements is smaller than the space of possible keys, that is to say, there exist several sets of public and private keys which will give the same DH agreement. To address this problem, we ‘hash in’ both parties' public keys to increase the ‘uniqueness’ of the shared secret.

Optionally, additional contextual information known by both parties can also be concatenated to the public keys and ‘hashed in’ to the secret, providing additional forward secrecy.

The shared secret is calculated by both parties as:

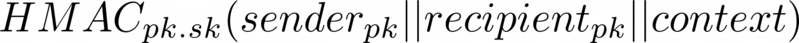
shared secret

Authenticated encryption is then achieved as described above, using the Xsalsa20 stream cipher with Poly1305 MAC (secretbox).

6.6 Hashing

Hashing is done using a Blake2b keyed hash, with a digest length of 32 bytes unless specified otherwise.

6.7 Key derivation

Curve25519 (encryption) keys can be derived from Ed25519 (signing) keys, in such a way that both secret and public components can be derived, meaning we only need to establish a signing keypair. This is very convenient as it reduces the amount of keys we need to manage, but it is regarded by many cryptographers as bad practice and is not recommended if it can be avoided.

7 Higher level cryptographic functions

7.1 ‘One Way Box’

This is used to encrypt a message allowing a given recipient to decrypt it without knowing the identity of the sender. This is useful because it reduces the metadata required to be carried with the message, obfuscating the identity of the sender from an eavesdropper.

Furthermore, it is useful for its one-way property. After the sender has created the message, they are not able to decrypt it themselves. This makes it particularly useful for encrypting shards, because if all the shard messages are retained on the device of the secret-owner after being sent out, it is important that they cannot be recovered by the secret-owner themselves, as this would otherwise comprise of an extra copy of the secret being stored in a single location.

For transport systems which use append-only logs, this is absolutely essential, as it is not possible to remove the sent messages.

It works by using an ephemeral keypair for the sender, rather than their long-term key which is normally used. The public key ephemeral key is included with the ciphertext, and the private key is discarded after being used a single time, and never stored on disk.

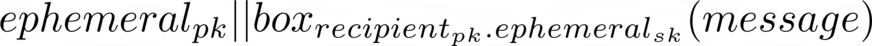
one way box

Since shards should always be signed with the long term signing key of the secret-owner, and are never transmitted without this signature, using an ephemeral key for encryption does not introduce any doubt as to the identity of the secret owner.

8 Shamir’s secret sharing

Unlike more commonly used cryptographic primitives, there is little standardisation for threshold-based secret sharing algorithms. Although there does exist a standardised scheme ‘SLIP39’, this protocol does not completely adhere to it. Rather, we use a C implementation ‘sss’ authored by Daan Sprenkles.

The reasoning behind this choice is explained in Choosing a threshold-based secret sharing algorithm.

‘sss’ has bindings for NodeJS, Go, Rust, and Webassembly, and includes a ‘submodule’ containing a secure random number generator.

Like many other secret sharing implementations, it uses a Lagrange interpolation on a 256 bit Galois field.

8.1 Authenticated encryption of secret

To ensure a uniformly random secret, as well as to enable integrity checking on recovery, the secret is not used directly in the secret sharing algorithm. Rather, a random key is generated, the secret is encrypted with this key using the authenticated symmetric encryption technique described above, and this key is taken to be the secret in the secret sharing algorithm. The ciphertext is concatenated to each share.

Secrets flow diagram

Share format: share-index||share||ciphertext

Although Daan Sprenkles' implementation includes this functionality, it restricts us to a 64 byte fixed length secret. In some cases, this might make the share size unnecessarily long (which could be an issue, for example if the shares are to be encoded as QR codes). In order to give more flexibility, to allow longer secrets such as RSA keys, as well as compact secrets, our standard allows a variable length secret, with optional padding for cases where it is important to obfuscate the secrets length.

8.2 Bit slicing

‘sss’ uses several techniques to protect against side channel attacks, including ‘bit slicing’. These types of attacks rely on factors such as timing or even physical properties such as CPU temperature, to derive knowledge otherwise unavailable to an attacker. For example a custodian might be able to derive something about the secret by repeatedly trying a combination of their own share and several random shares, and observing the time the algorithm takes to run.

Bit slicing, involves taking the two dimensional array of shares and ‘turning it on its side’ when doing the interpolation computations, and then re-orienting the result appropriately afterwards. This makes it near impossible to determine knowledge about individual shares by observing physical factors relating to the computation.

8.3 Zero-padding of secret

Zero padding of secret

The technique of using authenticated encryption and using the key in the secret sharing algorithm allows us to have a variable length secret. So any kind of key or data can be ‘sharded’ regardless of its size. However, it must be noted that the length of the secret can be determined by the length of a given share, so it is revealed to the custodian. In some situations this may be undesirable, for example when the secret is a password, or a particular kind of key with a characteristic length. A solution to this is to add padding, in order to make the secret have a constant length. For example a secret of length 32 could be padded with an additional 32 bytes, all of which are zero, to pad to a standard length of 64 bytes.

8.4 Obfuscation of the x-coordinate

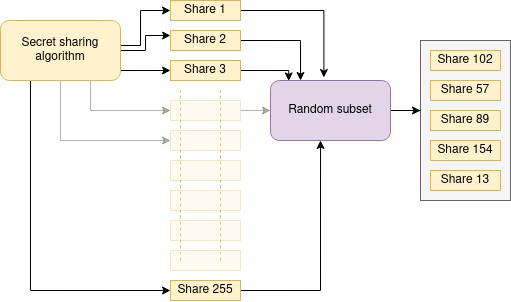
Random subset of shares

Shares are a collection of points on an array of parabolic curves, and contain both a ‘share index’, the x coordinate, which remains constant throughout the array, and the ‘share value’, an array of y coordinates. The share indexes are given a consecutive numbers for each share, so if we have 4 shares, they would have share indexes 1, 2, 3, and 4. This means that having a share gives some indication of the total number of shares. For example, if we have share number 3, we can infer that at least two other shares exist. To obfuscate this additional information, we generate a set of 255 shares and randomly select the desired amount of shares from this set. This means nothing can be inferred from knowing your own share value, other than that the number of shares is less than 255.

This is achieved using a ‘Durstenfeld schuffle’ algorithm, to shuffle the array of shares, but instead of completely shuffling the array, we take only the desired number of elements.

8.5 Including a label with the secret

This is an optional feature to indicate the intended purpose of the secret, meaning that it is still useful if recovered ‘out of context’. This will generally include a ‘label’ property which will be a human readable description, including, for example, the name of the application it was created with or the purpose. The label may also include application-specific data.

This feature is important because, as Pamela Morgan makes clear in her book ‘Crypto-asset inheritance planning’, recovering a key is only half the story. For it be useful, we need to know what to do with it. In some situations it makes less sense to include a descriptive label with the secret because the context in which the shares are stored gives us information about their intended use. For example, if they are shares of an email encryption key used in an email client, the fact that they are stored with the other files relating to this application is probably enough context to determine what they are for. However, if the shares are to be printed on paper as mnemonics or QR codes, it is less obvious.

The amount of information included in a label depends on how critical it is that share size is kept small, which varies with different applications.

If this feature is adopted, the secret should be encoded as a protocol buffer with two properties, the secret itself, stored in binary form, and the label stored as a string. Protocol buffers were chosen as the serialisation standard because it is widely adopted and implemented in many languages.

The protocol buffer schema for this message looks like this:

syntax = "proto2";

message Secret {
  required bytes secret = 1;
  optional string label = 2;
}

9 Anatomy of a shard

A shard consists of the share component (a share of the key to the secret), the encrypted secret component, and a signature. Including the share index, share, nonce, MAC, and signature mean the share length is 137 bytes, plus the length of the secret, or a standard length if zero-padding is used.

Anatomy of a shard

In many cases, it is useful to be able to add additional data to a secret without needing to distribute a new set of shares. In this case the share data can be separated from the encrypted secret data. So each custodian is sent one shard message and one or more encrypted backup messages.

Anatomy of separate shard and encrypted backup messages

10 Descriptions of modules used in the reference implementation

10.1 dark-crystal-shamir-secret-sharing

The secret sharing algorithm. This provides JNA bindings to the C library dsprenkels/sss.

10.2 dark-crystal-secret-sharing-wrapper

A wrapper around libSSS providing higher functionality specific to dark-crystal key backup, including:

  • Variable length secrets with authentication
  • Obfuscations of the x-coordinate (discussed below/above*)
  • Optional zero-padding

10.3 dark-crystal-key-backup-crypto-java

Contains cryptographic operations used for key backup and recovery.

10.4 dark-crystal-key-backup-message-schemas-java

Contains template schemas for Dark Crystal key backup messages, using protocol buffers, XML, and JSON.

11 Setup process

This section walks through the process making a distributed backup of a secret

11.1 Step 1 - Secret is combined with contextual metadata

secret and label

This step is optional and is to indicate the intended purpose of the secret, meaning that it is still useful if recovered ‘out of context’. This means including a ‘label’ property which will be a human readable description, including, for example, the name of the application it is useful for. This may also include application-specific data.

The amount of information included here depends on how critical it is that share size is kept small.

11.2 Step 2 - Encrypt data with symmetric key and Message Authentication Code added

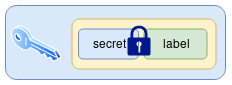
secret and label with key

The data is encrypted with a symmetric key and this key is taken to be the secret. Otherwise, the data itself is taken to be the secret. It needs to be noted that many implementations of secret sharing do this internally, and produce shares which are a concatenation of a key-share and the encrypted secret.

This means there is some duplication of data - a portion of each share is identical to the others. So in the case of particularly large secrets, it makes sense if the encrypted secret is stored only once in a place which is accessible to all share-holders (if the practicalities of the chosen transport/storage layer make this possible).

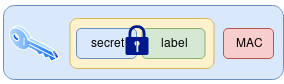
secret label key mac

A poly1305 MAC is used, which allows us to later verify that the secret has been correctly recovered.

11.3 Step 3 - Shards generated

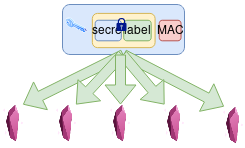
shards

Shards are generated using a secure threshold-based secret sharing algorithm, dsprenkels/sss

11.4 Step 4 - Shards are signed

Each shard is signed by the owner of the secret using a keypair with an established public key (such as the same keypair used to sign other messages in the application).

Shards are appended with these signatures, meaning the complete shard format looks like this:

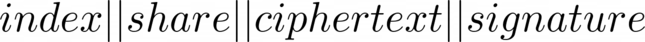
shard format

This is to protect against shards being modified, maliciously or accidentally, and achieves the same goal as schemes known as ‘Verifiable Secret Sharing’.

This is discussed in detail in our threat model report.

11.5 Step 5 - Schema version number and timestamp added

A version number ensures backward compatibility with future versions of the protocol.

A timestamp allows secret-owner and custodian to keep track of what happened when.

11.6 Step 6 - Signed shards encrypted for each custodian

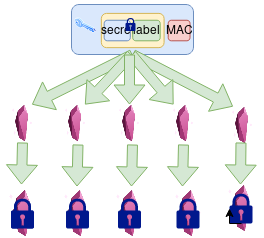
shards

Shards are encrypted with the public key of each custodian. The unencrypted shards are removed from memory.

‘One-way box’ is used to ensure the custodian can read the message, but the secret-owner cannot read it themselves.

This is inspired by private-box, see this note in the design document. We could also just use private-box itself for this, but this method is simpler and gives us smaller shards.

11.7 Step 7 - Transmission

Each encrypted shard is packed together with some metadata into a message, transmitted to the custodian, and a local (encrypted) copy is retained.

Additionally, a ‘root’ message is created which contains some metadata describing the secret. This message is retained locally and serves as a record of the backup.

Details of these messages, as well as of the system of requesting, responding, and forwarding shards, are explained in the message schemas section

12 Recovery process

This section walks through the process of recovering a secret from a distributed backup

12.1 Step 1 - New identity

Upon loss of data, the secret owner establishes a new account, giving them a new identity on the system. This step depends a lot on the transport mechanism used, but will generally involve generating a new keypair.

12.2 Step 2 - Contact custodians

The secret owner contacts the custodians ‘out of band’ to confirm that the new identity belongs to them. That is, it is assumed that there is the possibility of some personal contact to convince the custodians that the new identity is really the secret owner. For example this might involve a phone call saying “hey, its me!”.

Due to the threshold nature of the scheme there is a degree of tolerance to some custodians being unavailable or uncooperative.

The user interface should be designed to encourage the custodians to get the secret owner to confirm their new key out of band. If on a phone call, rather than trying to confirm some characters from the key itself, it can be much easier to confirm some dictionary words derived from the key.

12.3 Step 3 - Return shards

Each custodian decrypts the shard they are holding with their personal keypair, and re-encrypts it to the public key of the new account. It is then sent to the new account of the secret owner.

The nature peer to peer protocols makes it difficult to delete data. If this is the case with the transport mechanism you are using, we recommend adding a second layer of encryption using an ephemeral keypair. This is a single-use keypair which can later be deleted to effectively delete these messages from the system. This will be explained in more detail in a separate document.

12.4 Step 3 - Decrypt shards

The secret owner decrypts the shards they receive, using oneWayUnbox (described above).

12.5 Step 4 - Validate shards

validated shards

The signature of each shard is validated with the original public key, proving that the returned shards are identical to those sent out.

In the case that the shard could not be validated, the shard data can be retrieved anyway using detachMessage.

12.6 Step 5 - Secret recovery

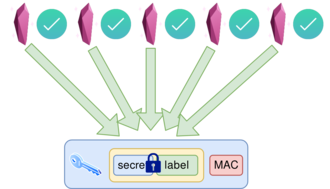
recovery

The shards are combined to recover the secret.

12.7 Step 6 - Validate secret

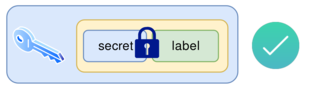
recovery successful

The MAC is used to establish that recovery was successful. This means we can be sure the combining process worked as planned and offers some protection against tampering.

12.8 Step 7 - Decrypt secret

secret and label

Finally the secret is restored, along with a descriptive label.

12.9 Step 8 - Recover original account

Depending on whether the lost account might have been compromised, it may be appropriate to abandon the new identity and continue to use the old one. If this is not the case, the key can at least be used to recover data encrypted to it.

In order to avoid confusion between the new ‘temporary’ identity, and the original one being restored, it may make sense, at the user-interface level, to restrict what a peer is able to with the application whilst they are in the process of retrieving shards from custodians. For example making clear that they are currently in ‘recovery mode’ and are not able to use the normal features of the application until either their original identity is restored, or they create a ‘normal’ new account.

13 Additional features

13.1 Shards of shards

Shards of shards

Shards held for others can be used as the secret, which gives an additional layer of tolerance to loss besides the threshold mechanism. That is, when you receive a shard from someone else, you distribute it to your own set of custodians. As described in section 9, anatomy of a shard, if the share data and encrypted secret are in separate messages, it is very easy to distribute additional secret data without needing to create a new set of shares.